
METODI DI RISOLUZIONE DEI SEGNALI BLOCCANTI
Ipotizziamo ora di considerare la sequenza costituita da due cilindri A e B, entrambi DE:
A+/B+/B-/A-
E ipotizziamo che tale sequenza debba avvenire in ciclo continuo.
Se scriviamo la logica che comanda ogni fase otteniamo:
◊ il cilindro A esce se è presente il selettore S e il finecorsa a0;
◊ il cilindro B esce se è presente il finecorsa a1;
◊ il cilindro B rientra se è presente il finecorsa b1;
◊ il cilindro A rientra se è presente il finecorsa b0;
Se cabliamo un circuito pneumatico con tale logica esso non parte neanche visto che si presentano delle situazioni di incertezza.
Infatti, in condizioni di riposo, cioè con gli steli nelle rispettive posizioni iniziali, sono attivi i finecorsa a0 e b0, se a questo punto attiviamo il selettore S sono soddisfatte contemporaneamente due logiche: quella che fa eseguire A+ e quella che fa eseguire A- e ciò porta ad una contraddizione.
Lo stesso problema si pone nel passaggio dalla seconda alla terza fase ( dove sono presenti i finecorsa a1 e b1 ) in cui sono soddisfatte entrambe le logiche di B+ e di B-.
Questo problema è causato dalla presenza di segnali cosiddetti bloccanti.
Sono definiti bloccanti i segnali attivi durante la doppia corsa di un cilindro, quindi nella nostra sequenza sono b0 che è bloccante rispetto ad a0 e a1 che è bloccante rispetto a b1.
Per risolvere queste situazioni di incertezza in certi casi è sufficiente riscrivere la logica considerando tutti i finecorsa che devono essere presenti per eseguire una fase, in questo caso otteniamo:
◊ il cilindro A esce se è presente il selettore S e il finecorsa a0 e il finecorsa b0;
◊ il cilindro B esce se è presente il finecorsa a1 e il finecorsa b0;
◊ il cilindro B rientra se è presente il finecorsa a1 e il finecorsa b1;
◊ il cilindro A rientra se è presente il finecorsa a1 e il finecorsa b0;
La sequenza in questo caso parte visto che all’inizio sono presenti i finecorsa a0 e b0 e attivando S l’unica logica soddisfatta è quella che fa eseguire A+, lo stesso discorso vale fra la fase due e la tre dove l’unica logica soddisfatta è quella di B-.
Il problema ora sta nel fatto che ci sono delle logiche ripetute, come si può notare B+ e A- sono comandate dagli stessi segnali quindi una volta partita la sequenza non evolve come desiderato, ma dopo la prima fase si eseguono immediatamente sia B+ che A-, questo metodo è quindi da escludere.
Il problema dei segnali bloccanti è risolvibile con diverse soluzioni.
La prima che consideriamo consiste nell’utilizzare dei finecorsa unidirezionali a salterello al posto di quelli che provocano i segnali bloccanti.
Questi finecorsa dovranno essere posizionati un po’ prima o un po’ dopo la fine della corsa del cilindro, in questo modo tali segnali non resteranno attivi durante la fermata dello stelo impedendo di bloccare la sequenza.
- Circuito con finecorsa a salterello (per scaricare la simulazione clicca qui)

Questo metodo presenta l’inconveniente di dare origine ad un leggero accavallamento di fasi, infatti, B esce quando si attiva il finecorsa unidirezionale a1, ma A non ha ancora concluso completamente la sua corsa proprio perché a1 è montato un po’ prima della fine della corsa.
Altro metodo è quello in cui si adottano limitatori di impulso che riducono la durata dei segnali bloccanti, eliminando quindi le situazioni di incertezza.
Ovviamente i limitatori dovranno essere inseriti all’uscita dei finecorsa bloccanti.
- Circuito con limitatori d’impulso per segnali bloccanti (per scaricare la simulazione clicca qui)
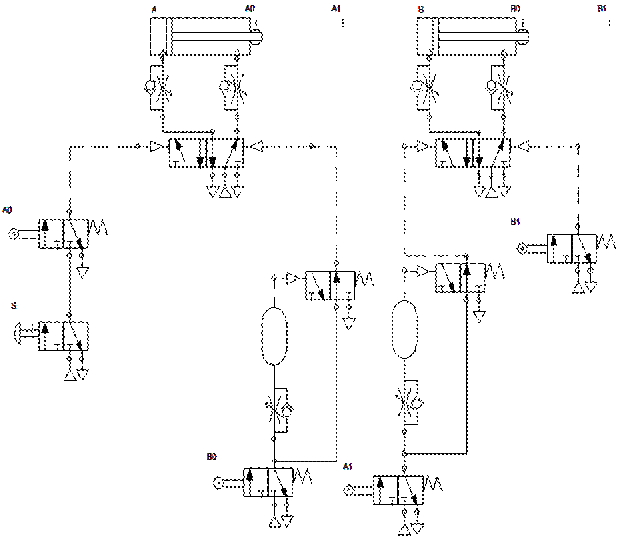
Un altro modo per risolvere sequenze con segnali bloccanti è ricorrere a memorie ausiliarie (4/2 o 5/2 bistabili) le quali alimentano i finecorsa che producono tali segnali solo in certi momenti e che vengono commutate tramite i segnali dei finecorsa precedenti a quelli bloccanti.
- Circuito con memoria ausiliaria e valvola distributrice bistabile (per scaricare la simulazione clicca qui)

In questo esempio b0 viene alimentato solo quando il finecorsa b1 va a commutare la memoria impedendo dunque che il segnale bloccante sia presente anche alla partenza dove andrebbe a bloccare l’uscita di A.
Lo stesso discorso vale per il finecorsa a1.
Il circuito con memoria ausiliaria può essere modificando adottando, al posto di una valvola distributrice bistabile una unistabile per i cilindri la cui doppia corsa avviene consecutivamente.
- Circuito con memoria ausiliaria e valvola distributrice unistabile (per scaricare la simulazione clicca qui)

In questo caso si ottiene la fuoriuscita di A semplicemente annullando il finecorsa bloccante b0, questo si ottiene come prima attraverso la memoria ausiliaria.
Con questi ultimi due metodi il numero delle memorie ausiliarie dipende dal numero di segnali bloccanti, per questo se si hanno sequenze un po’ più complesse il circuito può diventare molto complesso.
Per questo si può adottare il metodo cosiddetto della tecnica delle memorie in”cascata”.
Esso consta di vari punti:
◊ scrivere la sequenza e i finecorsa che controllano ogni fase;
◊ dividere la sequenza in gruppi di fasi, in modo che in ciascun gruppo non compaiano movimenti opposti consecutivi dello stesso cilindro;
◊ il numero di gruppi corrisponde al numero di linee che sono alimentate dalle memorie ausiliarie;
◊ il numero di memorie è pari al numero di gruppi meno uno;
◊ il finecorsa che controlla l’inizio della prima fase del primo gruppo viene alimentato dall’esterno;
◊ i finecorsa che controllano la prima fase di ogni gruppo (tranne il primo) vengono alimentati dalla linea precedente;
◊ gli altri finecorsa vengono alimentati dalla linea a cui appartengono;
◊ le memorie ausiliarie vengono commutate dai finecorsa in testa a ciascun gruppo e da un’uscita della memoria precedente;
◊ l’ alimentazione delle linee è controllata dalle memorie ausiliarie;
◊ la prima memoria è alimentata dall’esterno, le altre da un’uscita della memoria precedente.
Nel caso della sequenza A+/B+/B-/A- il circuito sarà uguale al metodo con memoria ausiliaria.
Nel caso della sequenza più complessa A+/A-/B+/C+/C-/D+/D-/B- dove sono presenti 5 segnali bloccanti, con il metodo delle memorie ausiliarie bisognerebbe utilizzare almeno 3 memorie, con la tecnica in cascata ne bastano due.
Infatti, se si divide la sequenza come segue ( utilizzando il minor numero di gruppi ), il circuito sarà: (per scaricare la simulazione clicca qui)

Tale sequenza è stata divisa in questo modo:
1° gruppo: D-/B-/A+
2° gruppo: A-/B+/C+
3° gruppo: C-/D+
e quindi la logica da cui si è ricavato il circuito è:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Uno degli strumenti più utilizzati per eseguire sequenze anche molto complesse è il sequenziatore.
Esso è costituito da un modulo per ogni fase più un modulo di “testa” e uno di “coda”.
Ogni modulo di fase contiene una memoria, un AND e un OR.
Il modulo di “testa” ha quattro entrate: l’alimentazione delle varie memorie, un ingresso che va ad entrare nella logica OR di tutti i moduli, uno che deve essere collegato al modulo di “coda” per permettere il reset dell’ultima memoria e uno che collegato al modulo di “coda” permette, insieme ad un’ulteriore logica ( pulsanti, selettori,… ), di settare la prima memoria.
Le memorie sono comandate da un SET, risultante dalla logica AND del modulo precedente, da un RESET risultante dalla logica OR e da un’unica uscita che ha un triplice compito: mandare il segnale ai distributori che controllano gli attuatori per far avvenire la fase relativa a quel modulo, alimentare la logica AND, alimentare la logica OR del modulo precedente.
Sostanzialmente il funzionamento del sequenziatore è il seguente: una volta settata una memoria essa manda in uscita un segnale che comanda gli attuatori, uno che entra nella logica AND che, insieme al finecorsa relativo alla fase attuale e agli altri segnali richiesti dalla logica, va a settare la memoria successiva ( in questo modo la fase successiva non avverrà finchè non si è conclusa la precedente ) e uno che entra nella logica OR ( eventualmente insieme ad un’emergenza ) che va a resettare la memoria precedente.
In questo modo la sequenza avviene con un solo segnale attivo per volta impedendo situazioni di ambiguità.
Per l’avviamento del sequenziatore bisogna però eseguire la cosiddetta operazione di riarmo che consiste nel resettare manualmente tutte le memorie ( tramite appositi pulsanti inseriti sui moduli ) tranne l’ultima che dovrà essere settata.
L’operazione di settaggio dell’ultima memoria avviene solitamente tramite un pulsante detto di avviamento e può essere effettuata quindi a distanza.
La sequenza A+/B+/B-/A- può essere risolta utilizzando un sequenziatore nel seguente modo: (per scaricare la simulazione clicca qui)
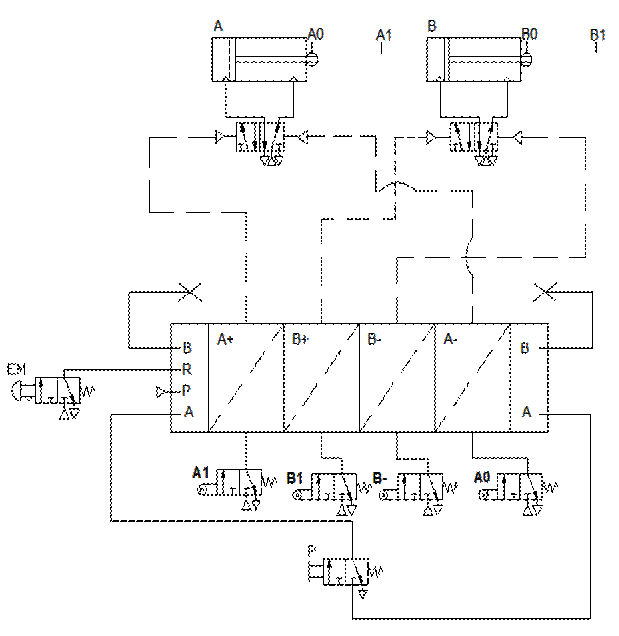
Conoscendo la struttura interna del sequenziatore si può simulare tale macchina in questo modo: (per scaricare la simulazione clicca qui)

Esistono inoltre dei moduli ausiliari che permettono l’esecuzione di sotto-programmi ripetuti durante una sequenza senza dover ricorrere ogni volta ad altri moduli di fase.
La sequenza A+/B+/B-/A-/B+/B- potrà essere così ottenuta: (per scaricare la simulazione clicca qui)
